第二条主宰的定律是菲克定律，描述粒子如何在空间中扩散。有点类似描述热传导的傅立叶定律，菲克定律说明了物质的质量通量(单位时间内通过单位面积的物质质量)会正比于浓度梯度，只是两者方向相反。质量通量和浓度梯度之间的比例就是扩散系数D，二氧化碳在水中的扩散系数约为2×109 m2/s。

当我们打开一瓶内含加压二氧化碳的液体，外压降低了，亨利定律告诉我们瓶内的任何小气室会马上降到相对应的饱和浓度；这样的改变产生了一个浓度梯度，于是气体开始流入小气室，使其成长为一颗气泡。

如果讨论的是一颗单独的球状气泡，那我们可以把两条定律合并为Epstein–Plesset方程式。我们若先把表面张力忽略掉，则方程式可以写成如下所示：

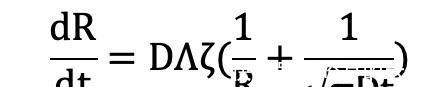
其中Λ是Ostwald常数，代表给定体积的气体能让多少液体达到饱和；ζ是过饱和程度；R则是气泡半径。这条方程式是一个重要的出发点，帮助我们接下来建立较复杂的模型，来描述汽相与液相间的质量交换关系。

它预测了气泡半径会因为扩散作用，随着时间的根号而成长。当气泡逐渐成长，要存活下来就必须找到一个可以帮助维持稳定的固定点，可能是大麦或啤酒花纤维素纤维中的空隙，抑或是玻璃杯上的小裂缝。

当气泡成长到某个大小，浮力足以使他们脱离原本诞生的结核点，气泡便会开始上升。气泡离开后，往往会在原本的地方留下一个小气室，下个小气泡便从这样的气室中诞生，形成一个循环。因为气泡的生命有这样的循环，所以我们在啤酒杯或香槟杯中，常可以看到许多向上流窜的泡泡排成一条整齐的队伍。

一旦进入这条稳定上升的道路，气泡的上升速度会随着半径增加。同时，由于气泡和周遭液体的相对速度增加，气体更快地从液相进入汽相，导致气泡成长的速率超越我们原本预期的时间根号正比。

三、湖底喷发

的确，从实验数据可以看到，在过饱和液体中，气泡的大小以固定的速率成长，也就是与时间成正比，而和气泡的尺寸无关。不过这并不是因为气泡周围的液压随着气泡在杯中深度而减少，在一个10 cm高的啤酒杯中，这种效应造成的变化大约只有外压的1%。

气泡的上升运动由两种力的抗衡所主宰：浮力与液体的黏滞阻力，其中浮力又与气泡体积成正比。由于气泡上升的速度大于二氧化碳回到液相的速率，这可以解释气泡为何会以固定的速率成长。对于水中尺寸较小的二氧化碳气泡，雷诺数(惯性力对黏滞力的比值)较小。

基于类似的道理，如果容器内的液体正在流动，尚未脱离容器壁的气泡也会成长的更快。饮料被倒入杯中之后，容器壁附近的液体对流促使气泡快速成长，气泡脱离后上升帮助液体对流持续进行，进而加快气泡的成长，形成一个正反馈，造成液体中溶解的二氧化碳大量流失。

就是这一连串的效应，才会导致啤酒或气泡酒中的气体在开瓶后很快跑光。如果我们单纯只考虑扩散效应，那么碳酸饮料中的气体跑光所需的时间大约是H2/D，其中H代表容器高度。在一个10 cm高的玻璃杯中，所需时间大约是5×106秒，也就是两个月。

在2005年，翰斯大学(University of Reims Champagne-Ardenne)的化学物理教授Gérard Liger-Belair指出饮料中的二氧化碳逸散远远不需这么多时间。尽管实际上由气泡所输送到表面的气体只占总量的20%，但是气泡上升引发的对流也会加快表面的水平流动。

另外，轻敲瓶子也能让饮料的气泡更快释出。这篇文章的作者其中一人Rodríguez-Rodríguez在四年前和他的同事发现，轻敲瓶子造成的冲击波会触发一团密集的气泡团形成，其中含有大概一百万个微小泡泡。这些气泡团不只在形状上跟爆炸后的蕈状云十分相似，而且他们在促进对流方面远比一般的个别泡泡有效。

实验结果证实，他们的确会加速流动，让溶解的气体更快流失。类似的现象在其他化学反应系统中也能见到。当产物比起反应物密度较低，或是温度较高，便可能发生所谓的湖底喷发。这个名字来自于当淡水湖底部的湖水因为地质或生物活动，达到二氧化碳过饱和。

文章来源：《高压物理学报》 网址: http://www.gywlxbzz.cn/zonghexinwen/2021/1018/613.html